DecisionTree

#deepLearning/decisionTree

决策树模型

分类决策树模型(Decision Tree)是一种描述对实例进行分类的树形结构，决策树由结点(node)和有向边(directed edge)组成，结点有两种类型:内部结点(internal node)和叶结点(leaf node)，内部结点表示一个特征或属性，叶结点表示一个类。

决策树是一种基本的分类和回归方法。它通过模拟人类决策过程来预测目标变量的值，是一种树形结构的模型，其中每个内部节点代表一个属性上的测试，每个分支代表测试的结果，而每个叶节点代表一个类别（在分类树中）或一个连续值（在回归树中）。决策树的主要优点是模型具有很好的可解释性，即人们可以很容易地理解模型的决策过程。

算法原理

• 数据准备 → 通过数据清洗和数据处理，将数据整理为没有缺省值的向量。
• 寻找最佳特征 → 遍历每个特征的每一种划分方式，找到最好的划分特征。
• 生成分支 → 划分成两个或多个节点。
• 生成决策树 → 对分裂后的节点分别继续执行 2-3 步，直到每个节点只有一种类别。
• 决策分类 → 根据训练决策树模型，将预测数据进行分类。

特征选择

决定用哪个特征来划分特征空间。
通过信息增益选取对训练数据具有分类能力的特征。

香农熵(entropy)

在信息论与概率统计中，熵(entropy)是表示随机变量不确定性的度量。设 $X$ 是一个取有限个值的离散随机变量，其概率分布为
$$
P(X=x_{i})=p_{i},\ i=1,2, \cdots ,n
$$
则随机变量 $X$ 的熵定义为

$$
H(X) = - \sum_{i=1}^{n}p_i \log_2{p_i}
$$
当随机变量只取两个值，例如$1，0$时，即 $X$ 的分布为
$$
P(X=1)=p \ , \quad P(X=0)=1-p \ ,\quad 0\le p\le1
$$
熵为
$$
H(p)=-p\log_{2}p-(1-p)\log_{2}(1-p)
$$
这时，熵 $H(p)$ 随概率 $p$ 变化的曲线

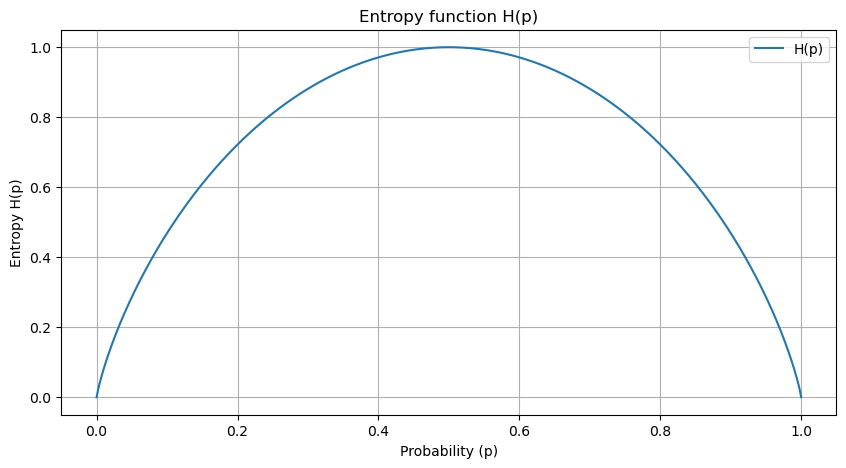
• 当 $p=0$ 或 $p=1$ 时 $H(p)=0$ ，随机变量完全没有不确定性。
• 当 $p=0.5$ 时 $H(p)=1$ ，熵取值最大，随机变量不确定性最大.

代码

def get_Ent(data):
    """
    参数:
    data -- 数据集

    返回:
    Ent -- 信息熵
    """
    # 计算信息熵
    num_sample = len(data)  # 样本个数
    label_counts = {}  # 初始化标签统计字典
    for i in range(num_sample):
        each_data = data.iloc[i, :]
        current_label = each_data["labels"]  # 得到当前元素的标签（label）

        # 如果标签不在当前字典中，添加该类标签并初始化 value=0,否则该类标签 value+1
        if current_label not in label_counts.keys():
            label_counts[current_label] = 0
        label_counts[current_label] += 1

    Ent = 0.0  # 初始化信息熵
    for key in label_counts:
        prob = float(label_counts[key])/num_sample
        Ent -= prob * math.log(prob, 2)  # 应用信息熵公式计算信息熵
    return Ent

条件熵 $H(Y|X)$

$X$ 给定条件下 $Y$ 的条件概率分布的熵对 $X$ 的数学期望
$$
\text{H}(D|A) = \sum_{j=1}^{n} \frac{|D_j|}{|D|} \text{H}(D_j)
$$
其中，$n$ 是属性 $A$ 的不同值的数目，$D_j$​ 是D中属性 $A$ 取第 $j$ 个值时的子集，$|D_j​|$ 是 $D_j$​ 的样本数量，$|D|$ 是 $D$ 的样本总数量。

信息增益

在划分数据集之前之后信息发生的变化称为信息增益，即划分前的信息熵减去划分后的信息熵。

信息增益 $g(D,A)$ 定义为集合 $D$ 的经验熵 $H(D)$ 与特征 $A$ 给定条件下 $D$ 的经验条件熵 $H(D|A)$ 之差，即
$$
Gain(D,A)=H(D)-H(D \mid A)
$$

信息增益（ID3）代码实现

def get_gain(data, base_ent, feature):
    """
    参数:
    data -- 数据集
    base_ent -- 根节点的信息熵
    feature -- 计算信息增益的特征

    返回:
    Ent -- 信息熵
    """
    # 计算信息增益
    feature_list = data[feature]  # 得到一个特征的全部取值
    unique_value = set(feature_list)  # 特征取值的类别
    feature_ent = 0.0

    for each_feature in unique_value:
        temp_data = data[data[feature] == each_feature]
        weight = len(temp_data)/len(feature_list)  # 计算该特征的权重值
        temp_ent = weight*get_Ent(temp_data)
        feature_ent = feature_ent+temp_ent

    gain = base_ent - feature_ent  # 信息增益
    return gain

在构建决策树（如C4.5决策树算法）时，信息增益比常被用来选择属性，因为它可以减少因属性值数量大而偏向于选择这些属性的倾向，从而选择更有区分能力的属性。

算法C4.5是算法ID3的改进版，它使用了信息增益和增益比两种选择算法，先选出信息增益高于平均水平的属性，然后再在这些属性中选择增益比最高的，作为最优划分属性。这样综合了信息增益和增益比的优点，可以取得较好的效果。

基尼指数 (Gini)

$$
{\mathrm{Gini}}(p)=\sum_{k=1}^{K}p_{k}(1-p_{k})=1-\sum_{k=1}^{K}p_{k}^{2}
$$
基尼指数就是在样本集中随机抽出两个样本不同类别的概率。当样本集越不纯的时候，这个概率也就越大，即基尼指数也越大。

用基尼指数计算信息增益的公式
$$
\text{Gain}(D, a) = \text{Gini}(D) - \sum_{i=1}^{n} \left( \frac{|D^i|}{|D|} \text{Gini}(D^i) \right)
$$
和信息增益计算方式类似，就是使用划分前样本集 $D$ 的基尼指数减去划分后子样本集 $D^i$ 的基尼指数加权和。

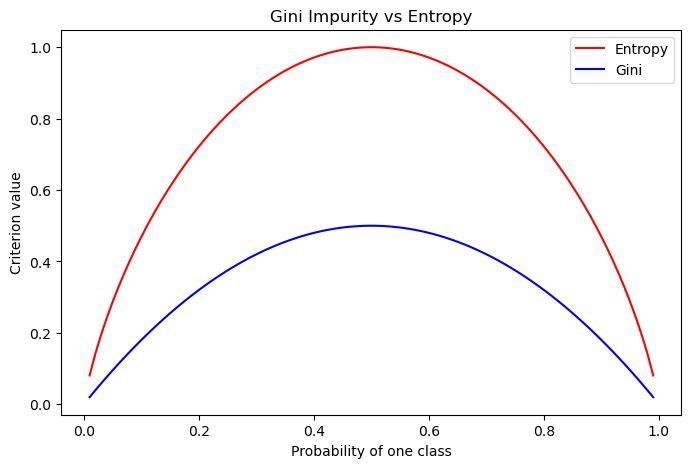
可以看出，基尼指数与信息熵虽然值不同，但是趋势一致。同样的，使用基尼指数来选择最优划分属性也是对比不同属性划分后基尼指数的差值，选择使样本集基尼指数减小最多的属性

决策树的生成

ID3 算法

ID3算法通过递归地选择具有最高信息增益的属性来构建决策树，直至所有实例属于同一类别或没有更多属性可用。

ID3算法的一个局限性在于它倾向于选择具有更多值的特征，这可能会导致决策树的过分生长，并且对噪声敏感。此外，ID3不直接处理连续特征和缺失值，并且生成的树只能用于分类，而不能用于回归问题。

具体步骤

选择最优特征：从当前样本集合的特征中，选择信息增益最大的特征作为节点特征，用于分支。
分支构造子集：根据选定的最优特征，把当前样本集分割成若干个子集，每个子集包含了数据集中所有在该特征上具有相同值的样本。
递归构造：对每个子集递归重复以上步骤，构造它们的决策子树，直到所有特征的信息增益均很小或者没有特征可以进行分割为止。

C4.5 的生成算法

C4.5算法是ID3的后续改进版本，它解决了ID3的一些局限性，包括使用信息增益率来选择特征，以及处理连续特征和缺失值的能力。C4.5还加入了剪枝步骤来减少过拟合问题。

信息增益比

特征 $A$ 对训练数据集 $D$ 的信息增益比 $g_R(D,4)$ 定义为其信息增益 $g(D,4)$ 与训练数据集 $D$ 的经验熵 $H(D)$ 之比:

$$
Gain_{-}ratio(D,a)=\frac{Gain(D,a)}{IV(a)}
$$
计算属性A的固有值（Intrinsic Value）:
固有值衡量的是属性A自身的信息熵，而不是属性A带来的信息增益。
$$
\text{IV}(A) = -\sum_{j=1}^{n} \frac{|D_j|}{|D|} \log_2 \frac{|D_j|}{|D|}
$$

其中，$n$ 是属性 $A$ 的不同值的数目，$D_j$ 是 $D$ 中属性 $A$ 取第 $j$ 个值时的子集，$|D_j|$ 是 $D_j$ 的样本数量，$|D|$ 是 $D$ 的样本总数量。

增益率对取值数目较少的属性会有所偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是是用了一个启发式: 先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

D3和C4.5算法的Python实现算法流程

算法流程

1. 决策树流程：
   获取训练集 $D$ 和特征集 $A$
   传入数据集D：计算$D$的经验熵
   计算个特征对数据集的信息增益（比）
   比较信息增益，选出最大值对应的特征
   根据特征将数据集 $D$ 划分为$D1、D2、…、Dn$
   判断$D_i$是否为一类：
   若是，则为一类
   若非，计算 $D_i$ 经验熵

2. 信息增益比
   循环求和：

• 获取属性B1所在行及长度：计算特征B的属性B1占所有数据比
• 计算数据集属性B1的信息熵
• 计算这二者的积，或计算每个A1占比*log2A1占比之差（即特征的值的熵）
• 特征B对数据集的信息增益=原数据集-和，或信息增益比=信息增益/特征的值的熵
• 对上面循环求解并比较每个特征对数据集的信息增益（比），求出最大值

from math import log
import operator

def createDataSet1():
    """
    创造示例数据/读取数据
    @param dataSet: 数据集
    @return dataSet labels：数据集 特征集
    """
    # 数据集
    dataSet = [('青年', '否', '否', '一般', '不同意'),
               ('青年', '否', '否', '好', '不同意'),
               ('青年', '是', '否', '好', '同意'),
               ('青年', '是', '是', '一般', '同意'),
               ('青年', '否', '否', '一般', '不同意'),
               ('中年', '否', '否', '一般', '不同意'),
               ('中年', '否', '否', '好', '不同意'),
               ('中年', '是', '是', '好', '同意'),
               ('中年', '否', '是', '非常好', '同意'),
               ('中年', '否', '是', '非常好', '同意'),
               ('老年', '否', '是', '非常好', '同意'),
               ('老年', '否', '是', '好', '同意'),
               ('老年', '是', '否', '好', '同意'),
               ('老年', '是', '否', '非常好', '同意'),
               ('老年', '否', '否', '一般', '不同意')]
    # 特征集
    labels = ['年龄', '有工作', '有房子', '信贷情况']
    
    return dataSet,labels

def calcShannonEnt(dataSet):
    """
    计算数据的熵(entropy)
    @param dataSet: 数据集
    @return shannonEnt: 数据集的熵
    """
    numEntries = len(dataSet)  # 数据条数
    
    # 循环判断每个样本的类别，统计每个类别的样本总数
    labelCounts = {}

    for featVec in dataSet:

        # 当前样本类型
        currentLabel = featVec[-1]  
        
        # 统计每个样本类型的数量
        try:
        	labelCounts[currentLabel] += 1
        except KeyError:
        	labelCounts[currentLabel] = 1
            
    # 根据公式计算香浓熵
    shannonEnt = 0
    
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob, 2)
        
    return shannonEnt
 
def splitDataSet(dataSet, index, value):
    """
    划分数据集，提取含有某个特征的某个属性的所有数据
    @param dataSet: 数据集
    @param index: 属性值所对应的特征列
    @param value: 某个属性值
    @return retDataSet: 含有某个特征的某个属性的数据集
    """
    
    retDataSet = []
    
    for featVec in dataSet:
        
        # 如果该样本该特征的属性值等于传入的属性值，则去掉该属性然后放入数据集中
        if featVec[index] == value:
            
            # 去掉该属性的当前样本
            reducedFeatVec = featVec[:index] + featVec[index+1:] 
            
            # append向末尾追加一个新元素，新元素在元素中格式不变，如数组作为一个值在元素中存在
            retDataSet.append(reducedFeatVec) 
    
    return retDataSet
 
def chooseBestFeatureToSplit(dataSet):
    """
    选择最优特征
    @param dataSet: 数据集
    @return bestFeature: 最优特征所在列
    """
    
    # 特征总数
    numFeatures = len(dataSet[0]) - 1 
    
    # 当只有一个特征时
    if numFeatures == 1:  
        return 0
    
    # 数据集的熵
    baseEntropy = calcShannonEnt(dataSet)  
    
    # 最佳信息增益比
    bestInfoGainRatio = 0 
    
    # 最优特征所在列
    bestFeature = -1 
    
    for i in range(numFeatures): 
        
        # 去重，每个属性值唯一
        uniqueVals = set(example[i] for example in dataSet) 
        
        # 定义按特征分类后的熵
        newEntropy = 0 
        
        # 定义特征的值的熵
        feaEntropy = 0 
        
        # 依次计算每个特征的值的熵
        for value in uniqueVals:
            # 根据该特征属性值分的类
            subDataSet = splitDataSet(dataSet,i,value) 
            
            # 参数：原数据、循环次数(当前属性值所在列)、当前属性值
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
            feaEntropy -= prob * log(prob, 2)
            
        # 信息增益比
        infoGainRatio = (baseEntropy - newEntropy) / feaEntropy 
        
        if (infoGainRatio > bestInfoGainRatio):
            bestInfoGainRatio = infoGainRatio
            bestFeature = i
            
    return bestFeature

def majorityCnt(classList):
    """
    对最后一个特征分类，出现次数最多的类即为该属性类别，比如：最后分类为2男1女，则判定为男
    @param classList: 数据集，也是类别集
    @return sortedClassCount[0][0]: 该属性的类别
    """
    
    classCount = {}
    
    # 计算每个类别出现次数
    for vote in classList:
        try:
            classCount[vote] += 1
        except KeyError:
            classCount[vote] = 1
            
    # 出现次数最多的类别在首位
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True) 
    
    # 对第1个参数，按照参数的第1个域来进行排序（第2个参数），然后反序（第3个参数）
    
    # 该属性的类别
    return sortedClassCount[0][0]

def createTree(dataSet,labels):
    """
    对最后一个特征分类，按分类后类别数量排序，比如：最后分类为2同意1不同意，则判定为同意
    @param dataSet: 数据集
    @param labels: 特征集
    @return myTree: 决策树
    """
    
    # 获取每行数据的最后一个值，即每行数据的类别
    classList = [example[-1] for example in dataSet]  

    # 当数据集只有一个类别
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    
    # 当数据集只剩一列（即类别），即根据最后一个特征分类
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    
    # 其他情况
    
    # 选择最优特征（所在列）
    bestFeat = chooseBestFeatureToSplit(dataSet) 
    
    # 最优特征
    bestFeatLabel = labels[bestFeat] 
    
    # 从特征集中删除当前最优特征
    del(labels[bestFeat]) 
    
    # 选出最优特征对应属性的唯一值
    uniqueVals = set(example[bestFeat] for example in dataSet) 
    
    # 分类结果以字典形式保存
    myTree = {bestFeatLabel:{}} 
    
    for value in uniqueVals:
        
        # 深拷贝，拷贝后的值与原值无关（普通复制为浅拷贝，对原值或拷贝后的值的改变互相影响）
        subLabels = labels[:] 
        
        # 递归调用创建决策树
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels) 
        
    return myTree
if __name__ == '__main__':
    
    # 创造示列数据
	dataSet, labels = createDataSet1()  
    
    # 输出决策树模型结果
	print(createTree(dataSet, labels))  

ID3算法的Python实现

根据上面的分析，将chooseBestFeatureToSplit函数中信息增益比的求解修改为信息增益的求解即可：

infoGainRatio= baseEntropy - newEntropy # 信息增益 修改第92行

由于infoGainRatio为信息增益比，infoGain才为信息增益

剪枝

预剪枝和后剪枝

在决策树的构建过程中，特别在数据特征非常多时，为了尽可能正确的划分每一个训练样本，结点的划分就会不停的重复，则一棵决策树的分支就非常多。对于训练集而言，拟合出来的模型是非常完美的。但是，这种完美就使得整体模型的复杂度变高，同时对其他数据集的预测能力下降，也就是我们常说的过拟合使得模型的泛化能力变弱。为了避免过拟合问题的出现，在决策树中最常见的两种方法就是预剪枝和后剪枝。

预剪枝

预剪枝，顾名思义预先减去枝叶，在构建决策树模型的时候，每一次对数据划分之前进行估计，如果当前节点的划分不能带来决策树泛化的提升，则停止划分并将当前节点标记为叶节点。例如前面构造的决策树，按照决策树的构建原则，通过 height 特征进行划分后 < 172分支中又按照 ear stud 特征值进行继续划分。如果应用预剪枝，则当通过 height 进行特征划分之后，对 < 172分支是否进行 ear stud 特征进行划分时计算划分前后的准确度，如果划分后的更高则按照 ear stud 继续划分，如果更低则停止划分。

后剪枝

跟预剪枝在构建决策树的过程中判断是否继续特征划分所不同的是，后剪枝在决策树构建好之后对树进行修剪。如果说预剪枝是自顶向下的修剪，那么后剪枝就是自底向上进行修剪。后剪枝将最后的分支节点替换为叶节点，判断是否带来决策树泛化的提升，是则进行修剪，并将该分支节点替换为叶节点，否则不进行修剪。例如在前面构建好决策树之后，>172分支的 voice 特征，将其替换为叶节点如（man），计算替换前后划分准确度，如果替换后准确度更高则进行修剪（用叶节点替换分支节点），否则不修剪。

CART 算法

CART 生成

CART 剪枝