损失函数

#deepLearning/LossFunction

均方差损失（Mean Square Error，MSE）

均方误差损失又称为二次损失、L2损失，常用于回归预测任务中。均方误差函数通过计算预测值和实际值之间距离（即误差）的平方来衡量模型优劣。即预测值和真实值越接近，两者的均方差就越小。

计算方式

假设有 $n$ 个训练数据 $x_i$，每个训练数据 $x_i$ 的真实输出为 $y_i$，模型对 $x_i$ 的预测值为 $\hat{y}_i$。该模型在 $n$ 个训练数据下所产生的均方误差损失可定义如下：

$$MSE=\frac{1}{n}\sum_{i=1}^n{\left( y_i-\hat{y}_i \right) ^2}$$
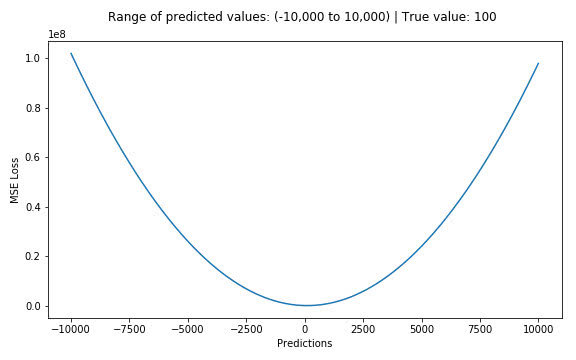
假设真实目标值为100，预测值在-10000到10000之间，我们绘制MSE函数曲线如 图 所示。可以看到，当预测值越接近100时，MSE损失值越小。MSE损失的范围为0到$\infty$ 。