Binary Tree

Posted on 2022-04-14 Edited on 2024-03-29 In C++ Word count in article: 4.8k Reading time ≈ 17 mins.

Binary Tree Practice

#algorithm/binaryTree

Binary Search Tree

// Binary Search Tree - Implemenation in C++
// Simple program to create a BST of integers and search an element in it 
#include<iostream>
using namespace std;
//Definition of Node for Binary search tree
struct BstNode {
 int data; 
 BstNode* left;
 BstNode* right;
};

// Function to create a new Node in heap
BstNode* GetNewNode(int data) {
 BstNode* newNode = new BstNode();
 newNode->data = data;
 newNode->left = newNode->right = NULL;
 return newNode;
}

// To insert data in BST, returns address of root node 
BstNode* Insert(BstNode* root,int data) {
 if(root == NULL) { // empty tree
  root = GetNewNode(data);
 }
 // if data to be inserted is lesser, insert in left subtree. 
 else if(data <= root->data) {
  root->left = Insert(root->left,data);
 }
 // else, insert in right subtree. 
 else {
  root->right = Insert(root->right,data);
 }
 return root;
}
//To search an element in BST, returns true if element is found
bool Search(BstNode* root,int data) {
 if(root == NULL) {
  return false;
 }
 else if(root->data == data) {
  return true;
 }
 else if(data <= root->data) {
  return Search(root->left,data);
 }
 else {
  return Search(root->right,data);
 }
}
int main() {
 BstNode* root = NULL;  // Creating an empty tree
 /*Code to test the logic*/
 root = Insert(root,15); 
 root = Insert(root,10); 
 root = Insert(root,20);
 root = Insert(root,25);
 root = Insert(root,8);
 root = Insert(root,12);
 // Ask user to enter a number.  
 int number;
 cout<<"Enter number be searched\n";
 cin>>number;
 //If number is found, print "FOUND"
 if(Search(root,number) == true) cout<<"Found\n";
 else cout<<"Not Found\n";
}

Level Order Traversal

// Function to print Nodes in a binary tree in Level order
void LevelOrder(Node *root)
{
    if (root == NULL)
        return;
    queue<Node *> Q;
    Q.push(root);
    // while there is at least one discovered node
    while (!Q.empty())
    {
        Node *current = Q.front();
        Q.pop(); // removing the element at front
        cout << current->data << " ";
        if (current->left != NULL)
            Q.push(current->left);
        if (current->right != NULL)
            Q.push(current->right);
    }
}

Source Code

/* Binary tree - Level Order Traversal */
#include <iostream>
#include <queue>
using namespace std;

struct Node
{
    char data;
    Node *left;
    Node *right;
};

// Function to print Nodes in a binary tree in Level order
void LevelOrder(Node *root)
{
    if (root == NULL)
        return;
    queue<Node *> Q;
    Q.push(root);
    // while there is at least one discovered node
    while (!Q.empty())
    {
        Node *current = Q.front();
        Q.pop(); // removing the element at front
        cout << current->data << " ";
        if (current->left != NULL)
            Q.push(current->left);
        if (current->right != NULL)
            Q.push(current->right);
    }
}
// Function to Insert Node in a Binary Search Tree
Node *Insert(Node *root, char data)
{
    if (root == NULL)
    {
        root = new Node();
        root->data = data;
        root->left = root->right = NULL;
    }
    else if (data <= root->data)
        root->left = Insert(root->left, data);
    else
        root->right = Insert(root->right, data);
    return root;
}

int main()
{
    /*Code To Test the logic
      Creating an example tree
                M
               / \
              B   Q
             / \   \
            A   C   Z
    */
    Node *root = NULL;
    root = Insert(root, 'M');
    root = Insert(root, 'B');
    root = Insert(root, 'Q');
    root = Insert(root, 'Z');
    root = Insert(root, 'A');
    root = Insert(root, 'C');
    // Print Nodes in Level Order.
    LevelOrder(root);
}

Binary Tree Traversal

PreOrder

// Function to visit nodes in Preorder
void Preorder(struct Node *root)
{
    // base condition for recursion
    // if tree/sub-tree is empty, return and exit
    if (root == NULL)
        return;

    printf("%c ", root->data); // Print data
    Preorder(root->left);      // Visit left subtree
    Preorder(root->right);     // Visit right subtree
}

InOrder

// Function to visit nodes in Inorder
void Inorder(Node *root)
{
    if (root == NULL)
        return;

    Inorder(root->left);       // Visit left subtree
    printf("%c ", root->data); // Print data
    Inorder(root->right);      // Visit right subtree
}

PostOrder

// Function to visit nodes in Postorder
void Postorder(Node *root)
{
    if (root == NULL)
        return;

    Postorder(root->left);     // Visit left subtree
    Postorder(root->right);    // Visit right subtree
    printf("%c ", root->data); // Print data
}

Source Code

/* Binary Tree Traversal - Preorder, Inorder, Postorder */
#include <iostream>
using namespace std;

struct Node
{
    char data;
    struct Node *left;
    struct Node *right;
};

// Function to visit nodes in Preorder
void Preorder(struct Node *root)
{
    // base condition for recursion
    // if tree/sub-tree is empty, return and exit
    if (root == NULL)
        return;

    printf("%c ", root->data); // Print data
    Preorder(root->left);      // Visit left subtree
    Preorder(root->right);     // Visit right subtree
}

// Function to visit nodes in Inorder
void Inorder(Node *root)
{
    if (root == NULL)
        return;

    Inorder(root->left);       // Visit left subtree
    printf("%c ", root->data); // Print data
    Inorder(root->right);      // Visit right subtree
}

// Function to visit nodes in Postorder
void Postorder(Node *root)
{
    if (root == NULL)
        return;

    Postorder(root->left);     // Visit left subtree
    Postorder(root->right);    // Visit right subtree
    printf("%c ", root->data); // Print data
}

// Function to Insert Node in a Binary Search Tree
Node *Insert(Node *root, char data)
{
    if (root == NULL)
    {
        root = new Node();
        root->data = data;
        root->left = root->right = NULL;
    }
    else if (data <= root->data)
        root->left = Insert(root->left, data);
    else
        root->right = Insert(root->right, data);
    return root;
}

int main()
{
    /*Code To Test the logic
      Creating an example tree
                M
               / \
              B   Q
             / \   \
            A   C   Z
    */
    Node *root = NULL;
    root = Insert(root, 'M');
    root = Insert(root, 'B');
    root = Insert(root, 'Q');
    root = Insert(root, 'Z');
    root = Insert(root, 'A');
    root = Insert(root, 'C');
    // Print Nodes in Preorder.
    cout << "Preorder: ";
    Preorder(root);
    cout << "\n";
    // Print Nodes in Inorder
    cout << "Inorder: ";
    Inorder(root);
    cout << "\n";
    // Print Nodes in Postorder
    cout << "Postorder: ";
    Postorder(root);
    cout << "\n";
}

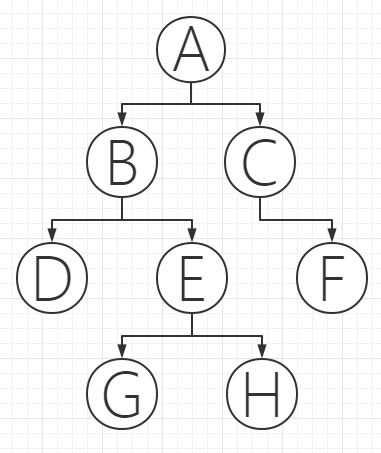
144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历

示例 1：

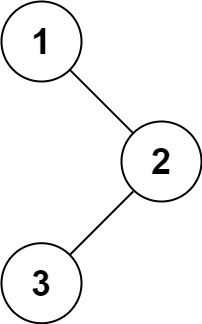
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

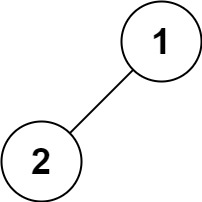
输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

Source Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void preorder(TreeNode *root, vector<int> &res){
        if(!root)return;
        res.push_back(root->val);
        preorder(root->left, res);
        preorder(root->right, res);
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> a;
        preorder(root, a);
        return a;
    }
};

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历

示例 1：

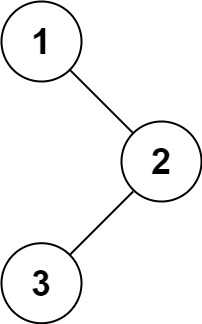
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

Source Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode *root, vector<int> &a){
        if(!root)return;
        inorder(root->left, a);
        a.push_back(root->val);
        inorder(root->right, a);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> a;
        inorder(root, a);
        return a;
    }
};

145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历

示例 1：

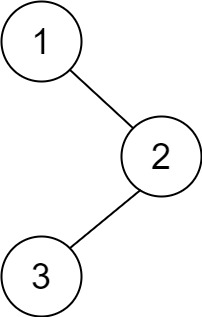
输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

Source Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void postorder(TreeNode *root, vector<int> &a){
        if(!root)return;
        postorder(root->left, a);
        postorder(root->right, a);
        a.push_back(root->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> a;
        postorder(root, a);
        return a;
    }
};

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历

示例 1：

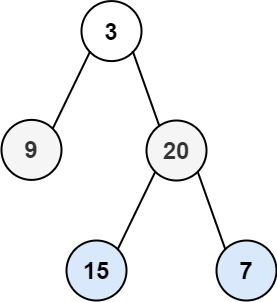
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

Source Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public: 
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> a;
        queue<TreeNode*> Q;
        if(!root)return a;
        Q.push(root);
        while(!Q.empty()){
            int Qsize = Q.size();
            a.push_back(vector<int>());
            for(int i = 0; i < Qsize; i++){
                TreeNode *tmp = Q.front();
                Q.pop();
                a.back().push_back(tmp->val);
                if(tmp->left)Q.push(tmp->left);
                if(tmp->right)Q.push(tmp->right);
            }
        }
        return a;
    }
};

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例： 给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3

source code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

//DFS
class Solution {
public:
    int res = 0, depth = 0;
    int maxDepth(TreeNode* root) {
        traverse(root);
        return res;
    }
    void traverse(TreeNode* root){
        if(!root)return;
        depth++;
        if(!root->left && !root->right)res = max(res, depth);
        traverse(root->left);
        traverse(root->right);
        depth--;
    }
};

//recursion
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root)return 0;
        int n = maxDepth(root->left);
        int m = maxDepth(root->right);
        return max(n, m) + 1;
    }
};

543.二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 : 给定二叉树

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

source code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxdiameter = 0;
    int diameterOfBinaryTree(TreeNode* root) {
        FindMaxDepth(root);
        return maxdiameter;
    }
    int FindMaxDepth(TreeNode* root){
        if(!root)return 0;
        int LeftMax = FindMaxDepth(root->left);
        int RightMax = FindMaxDepth(root->right);
        maxdiameter = max(maxdiameter, LeftMax + RightMax);
        return max(LeftMax, RightMax) + 1;
    }
};

226.翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

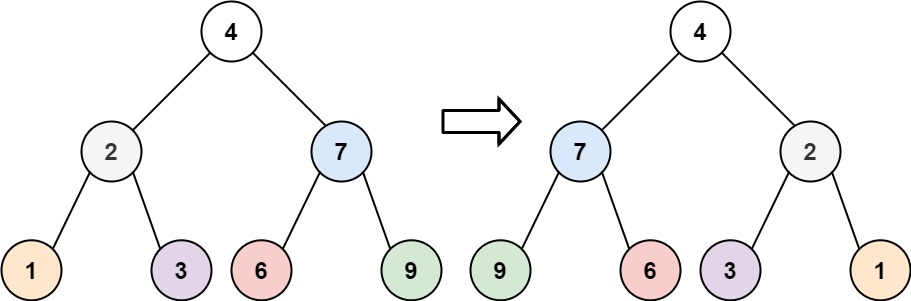
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

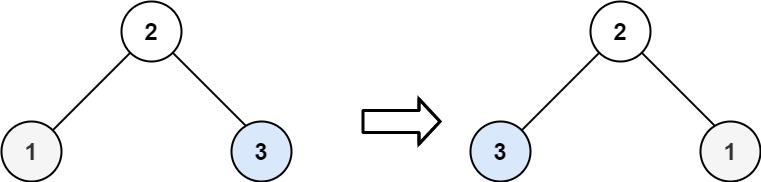
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

source code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution { //Solution 1
public:
    TreeNode* invertTree(TreeNode* root) {
        invert(root);
        return root;
    }
    void invert(TreeNode* root){
        if(!root)return;
        swap(root->left, root->right);
        invert(root->left);
        invert(root->right);
    }
};

class Solution { //Solution 2
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root)return NULL;
        TreeNode *left = invertTree(root->left);
        TreeNode *right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};

116.填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

提示：

树中节点的数量在 [0, 212 - 1] 范围内
-1000 <= node.val <= 1000

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

source code

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        if(!root)return NULL;
        traverse(root->left, root->right);
        return root;
    }
    void traverse(Node* node1, Node* node2){
        if(!node1 || !node2)return; 
        node1->next = node2;
        traverse(node1->left, node1->right);
        traverse(node2->left, node2->right);
        traverse(node1->right, node2->left);
    }
};

114.二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

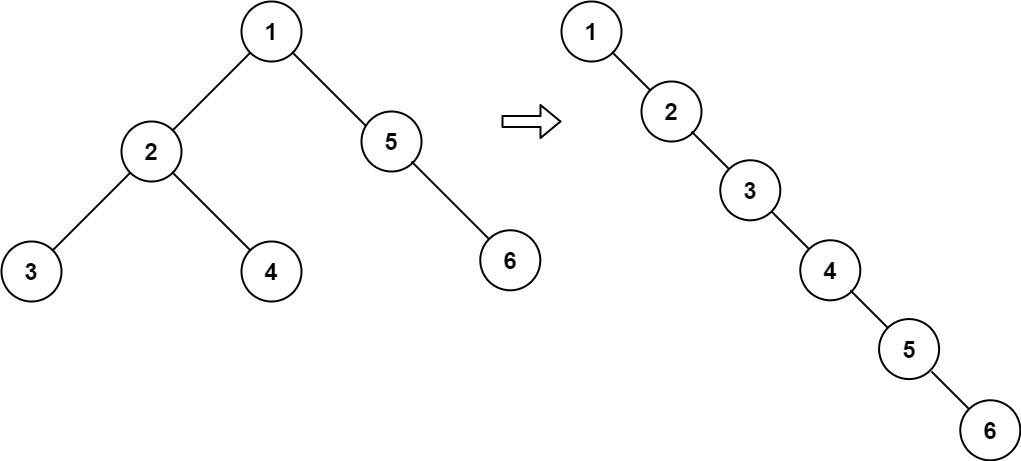
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

source code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if(!root)return;
        
        flatten(root->left);
        flatten(root->right);

        TreeNode *left = root->left;
        TreeNode *right = root->right;

        root->left = NULL;
        root->right = left;

        TreeNode *p = root;
        while(p->right)p = p->right;
        p->right = right;
    }
};

class Solution {
    //pre作为构建链表的辅助指针，在构建链表的过程，一直指向并维护当前链表“有效的”最末尾的节点
    //首先，初始化时，pre指向链表的虚拟头节点
    TreeNode pre = new TreeNode();

    public void flatten(TreeNode root) {
        //如果root为null，不用展开，跳出递归
        if(root == null) {
            return;
        }

        //“有效的”最末节点变更为root
        pre.right = root;
        pre.left = null;
        pre = pre.right;
        
        TreeNode temp = root.right;
        //展开左子树，在展开的过程中pre会一直指向并维护“有效的”最末节点
        flatten(root.left);
        //展开右子树，在展开的过程中pre会一直指向并维护“有效的”最末节点
        flatten(temp);
        //注意，由于是前序遍历，且pre要一直维护“有效的”最末节点，所以必须先展开左子树，然后才能展开右子树
    }
}

589. N 叉树的前序遍历

给定一个 n 叉树的根节点 root ，返回其节点值的前序遍历。

n 叉树在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6] 输出：[1,3,5,6,2,4]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：[1,2,3,6,7,11,14,4,8,12,5,9,13,10]

提示：

节点总数在范围 [0, 104]内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

思路：

对于二叉树来说，前序遍历的顺序为：根 - 左 - 右

推广到 N 叉树，顺序是先访问根节点，再依次递归其 children 数组中的节点（子树）

source code

class Solution {
    public List<Integer> preorder(Node root) {
        List<Integer> ans = new ArrayList<>();
        dfs(root, ans);
        return ans;
    }

    private void dfs(Node node, List<Integer> ans) {
        if (node == null) {
            return;
        }
        ans.add(node.val);
        for (Node c : node.children) {
            dfs(c, ans);
        }
    }
}

590. N 叉树的后序遍历

给定一个 n 叉树的根节点 root ，返回其节点值的 后序遍历 。

n 叉树在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[5,6,3,2,4,1]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[2,6,14,11,7,3,12,8,4,13,9,10,5,1]

提示：

节点总数在范围 [0, 104] 内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

source code

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<Integer> postorder(Node root) {
        List<Integer> ans = new ArrayList<>();
        loop(root, ans);
        return ans;
    }
    
    void loop(Node root, List<Integer> ans){
        if(root == null) return;
        for(Node node : root.children){
            loop(node, ans);
        }
        ans.add(root.val);
    }
}

889. 根据前序和后序遍历构造二叉树

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中任何一个。

示例 1：

输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

示例 2:

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

1 <= preorder.length <= 30
1 <= preorder[i] <= preorder.length
preorder 中所有值都不同
postorder.length == preorder.length
1 <= postorder[i] <= postorder.length
postorder 中所有值都不同
保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

思路:

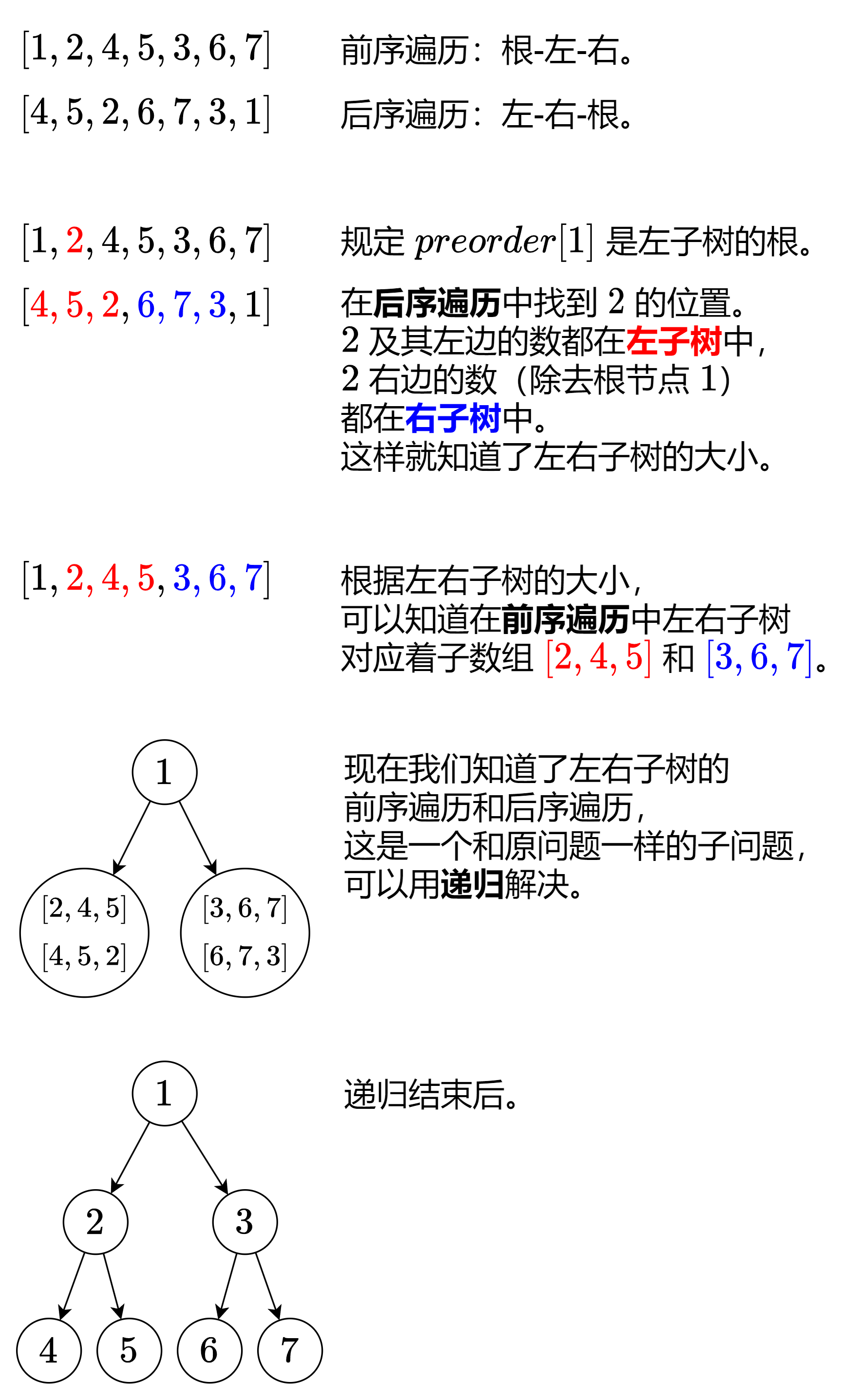
前序遍历：按照「根-左子树-右子树」的顺序遍历二叉树。

后序遍历：按照「左子树-右子树-根」的顺序遍历二叉树。

如果只知道前序遍历和后序遍历，这棵二叉树不一定是唯一的。

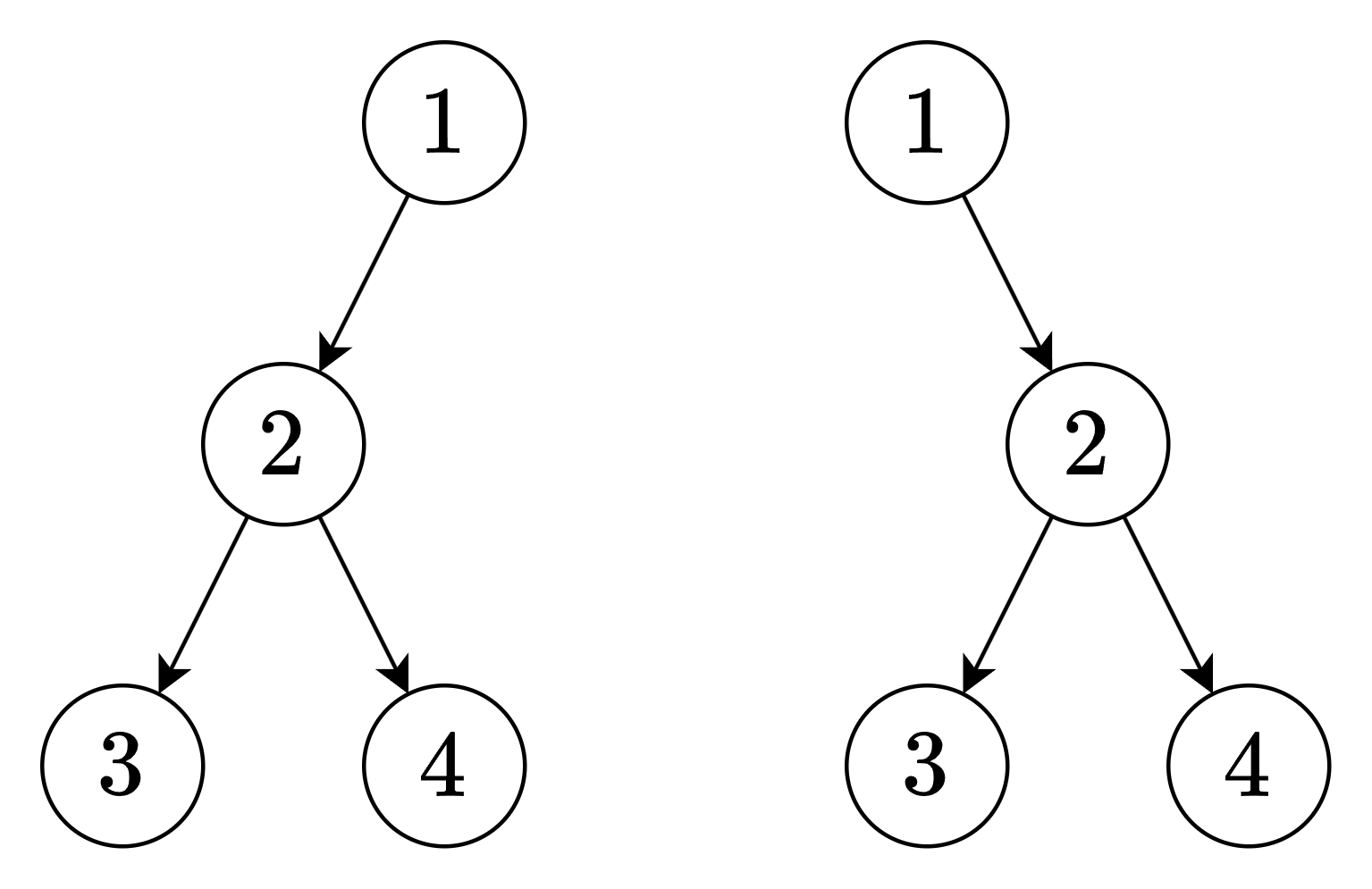
对于这两棵二叉树：

前序遍历都是 [1,2,3,4] 后序遍历都是 [3,4,2,1] 注：如果二叉树的每个非叶节点都有两个儿子，知道前序和后序就能唯一确定这棵二叉树。

题目说，如果存在多个答案，我们可以返回其中任何一个。那么不妨规定：无论什么情况，在前序遍历中，\(\textit{preorder}[1]\) 是左子树的根节点值。

递归边界：

如果 \(\textit{preorder}\) 的长度是 0，对应着空节点，返回空。如果 \(\textit{preorder}\) 的长度是 1，对应着二叉树的叶子，创建一个叶子节点并返回。

source code

class Solution {
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
           int n = preorder.length;
           if(n == 0){
               return null;
           }
           if(n == 1){
               return new TreeNode(preorder[0]);
           }
           int leftSize = indexOf(postorder, preorder[1]) + 1;
           int[] preorderL = Arrays.copyOfRange(preorder, 1, 1 + leftSize);
           int[] preorderR = Arrays.copyOfRange(preorder, 1 + leftSize, n);
           
           int[] postorderL = Arrays.copyOfRange(postorder, 0, leftSize);
           int[] postorderR = Arrays.copyOfRange(postorder, leftSize, n - 1);

           TreeNode left = constructFromPrePost(preorderL, postorderL);
           TreeNode right = constructFromPrePost(preorderR, postorderR);

           return new TreeNode(preorder[0], left, right);
    }

    int indexOf(int[] a, int x){
        for(int i = 0;; i ++){
            if(a[i] == x)return i;
        }
    }
}

复杂度分析时间复杂度：\(\mathcal{O}(n^2)\)，其中 n 为 \(\textit{preorder}\) 的长度。最坏情况下二叉树是一条链，我们需要递归 \(\mathcal{O}\) 次，每次都需要 \(\mathcal{O}(n)\) 的时间查找 \(\textit{preorder}[1]\) 和复制数组。空间复杂度：\(\mathcal{O}(n^2)\)

class Solution {
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        int n = preorder.length;
        int[] index = new int[n + 1];

        for (int i = 0; i < n; i++) {
            index[postorder[i]] = i;
        }
        
        return dfs(preorder, 0, n, postorder, 0, n, index); // 左闭右开区间
    }

    private TreeNode dfs(int[] preorder, int preL, int preR, int[] postorder, int postL, int postR, int[] index) {
        if (preL == preR) { // 空节点
            return null;
        }
        if (preL + 1 == preR) { // 叶子节点
            return new TreeNode(preorder[preL]);
        }
        
        int leftSize = index[preorder[preL + 1]] - postL + 1; // 左子树的大小

        TreeNode left = dfs(preorder, preL + 1, preL + 1 + leftSize, postorder, postL, postL + leftSize, index);
        TreeNode right = dfs(preorder, preL + 1 + leftSize, preR, postorder, postL + leftSize, postR - 1, index);
        
        return new TreeNode(preorder[preL], left, right);
    }
}

复杂度分析 时间复杂度：\(\mathcal{O}(n)\)，其中 n 为 \(\textit{preorder}\) 的长度。递归 \(\mathcal{O}(n)\) 次，每次只需要 \(\mathcal{O}(1)\) 的时间。空间复杂度：\(\mathcal{O}(n)\)。

左子树的重构：

TreeNode left = dfs(preorder, preL + 1, preL + 1 + leftSize, postorder, postL, postL + leftSize, index);

- preL + 1：在前序遍历中，根节点之后的第一个元素是左子树的根节点，因此这里从 preL + 1 开始。 - preL + 1 + leftSize：这是左子树在前序遍历数组中的结束位置。leftSize 是通过后序遍历数组计算得到的左子树的大小，因此 preL + 1 + leftSize 是左子树在前序遍历数组中的右边界（不包括）。 - postL 和 postL + leftSize：在后序遍历数组中，从 postL 开始到 postL + leftSize（不包括）是左子树的范围。

右子树的重构：

TreeNode right = dfs(preorder, preL + 1 + leftSize, preR, postorder, postL + leftSize, postR - 1, index);

- preL + 1 + leftSize：这是右子树在前序遍历数组中的开始位置，即左子树之后的第一个元素。 - preR：这是前序遍历数组的右边界（不包括）。 - postL + leftSize 和 postR - 1：在后序遍历中，右子树开始于左子树结束的位置，结束于整个树的根节点之前，因为在后序遍历中，根节点是最后访问的。

938. 二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32

示例 2：

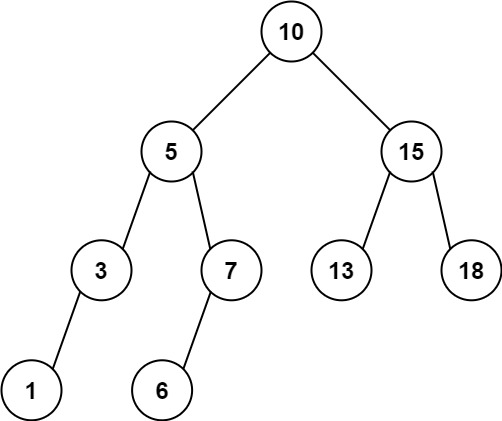
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

提示：

树中节点数目在范围 [1, 2 * 104] 内
1 <= Node.val <= 105
1 <= low <= high <= 105
所有 Node.val 互不相同

思路： - 标签：深度优先遍历 - 题意：这个题字面含义很难理解，本意就是求出所有 X >= L 且 X <= R 的值的和 - 递归终止条件： - 当前节点为 null 时返回 0 - 当前节点 X < L 时则返回右子树之和 - 当前节点 X > R 时则返回左子树之和 - 当前节点 X >= L 且 X <= R 时则返回：当前节点值 + 左子树之和 + 右子树之和注意点：通过判断X的大小能够避免遍历全部树的节点

source code

class Solution {
    public int rangeSumBST(TreeNode root, int low, int high) {
        if(root == null)return 0;

        if(root.val < low)return rangeSumBST(root.right, low, high);
        if(root.val > high)return rangeSumBST(root.left, low, high);

        int left = rangeSumBST(root.left, low, high);
        int right = rangeSumBST(root.right, low, high);

        return root.val + left + right;
    }
}```


# [101. 对称二叉树](https://leetcode.cn/problems/symmetric-tree/)


给你一个二叉树的根节点 `root` ， 检查它是否轴对称。

**示例 1：**

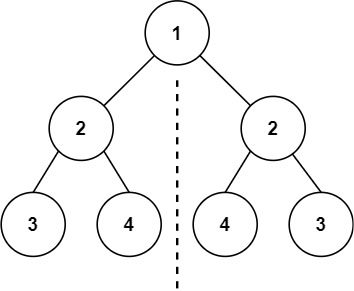
![](https://images-a2q.pages.dev/file/9adbc64a8dc1fe7537212.png)

输入：root = [1,2,2,3,4,4,3] 输出：true


**示例 2：**

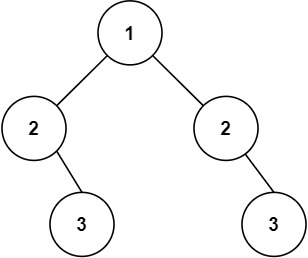
![](https://images-a2q.pages.dev/file/39c323a6b52636dcaf7c2.png)

输入：root = [1,2,2,null,3,null,3] 输出：false ```

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

source code ```java class Solution { public boolean isSymmetric(TreeNode root) { if(root == null)return true; return dfs(root.left, root.right); }

boolean dfs(TreeNode left, TreeNode right){
    if(left == null && right == null)return true;
    if(left == null || right == null)return false;
    if(left.val != right.val)return false;
    return dfs(left.left, right.right) && dfs(left.right, right.left);
}

}```